A smart manager will carefully choose members of a team to work together, trying to maximize the team’s proficiency without compromising the quality of the team’s work or its delivery to customers, according to the guidelines laid out in the first part of this series. The general technique of gaining proficiency through the continuous apprenticeship of team members is not difficult to understand, but making it measurable and optimizing skill acquisition can be elusive.
In this second part of the multipart series, the mathematical basis for skill acquisition through pairing team members together will be laid out, and reduced to some simpler guidelines.
Figuring Out Who Should Work With Who
Before I begin, there are a few assumptions that should be made. I’m talking about pairing, that is the arrangement of two people working together on a task. I’ll look at breaking with some of the exceptions in the next part of the series, but for now I’ll draw a few lines in the sand to make talking about things a little easier.
• Where are the Team Members?
The first thing to consider is whether or not a team is all in the same place - it strongly affects the effectiveness of pairing.
When a team is not all in one place, things can become quite constrained. If a team is broken up across different geographic regions, it may need to be treated as several separate teams. Or perhaps the team has individual members that are isolated - it may make pairing impossible, limiting skill acquisition to play and listening, or just taking an occasional class.
• Can a Dispersed Team be Brought Together?
For some teams, remote pairing may be possible. Over the last decade, the Internet has given some workers the ability to meet, share notes and work together across the wire. While this may not be as easy as working with each other face-to-face, it has become the standard for many, allowing team members considerable freedom in their personal lives that they might otherwise not enjoy.
When team members can be connected using the Internet, a geographically distributed group can be treated as a single team since anyone can pair with anyone else - figuring out pairing is done with everyone in the mix.
• Is there Enough of Everything?
This discussion focusses on a single team that can be assigned tasks that pairs can work on, that the composition of the work is well-determined, and that there is no shortage of this work. If there is slack built into the team’s schedule that can be used for playing to learn, so much the better, but I am assuming that there are skills that must be acquired and work that team members can do together.
• Are You a Smart Manager?
I’m going to assume I’m targeting a smart manager - if you’re a manager and you’re with me so far, you qualify. If you’re not a manager, you’ll still be able to help by managing your manager - give it a shot. Remember, smart managers work for their teams, not the other way around. They challenge their teams with interesting work, move away roadblocks, deal with reporting their progress upward, and help the members grow their skills while they have fun doing it.
So with that, there are things that are manageable, and things that aren’t.
What’s Not Manageable?
There are three sets of things being managed:
- M, the set of members of the team,
- S, the set of skills to be acquired, and
- W, the set of tasks to be worked on.
The items in these sets must each be addressed individually. Since the interrelations between the items in the sets can be complex, very different outcomes may occur when only slightly different decisions are made. The goal is to achieve the appropriate growth in skill proficiency across the team while its assigned work continues to be completed.
Skill Acquisition
To understand how learning occurs when two team members pair, a model must be created to represent how they transfer their skills to each other.
When two members are assigned to work together on a task, each take a short amount of time to find their respective place. The learning generally starts out slowly. If they’ve worked together before, or if their personalities mesh, it may begin more quickly. Eventually through working together, their proficiencies in the skills being used will increase to a sustained rate. If they pair long enough, as the proficiency of a member approaches a personal maximum for a skill, learning will taper off and remain at that high for as long as the skill is in use. Proficiency will hold, with pairing acting to reinforce the level that has been reached.
If proficiency is measured against time, the general shape of the skill learning curve is then
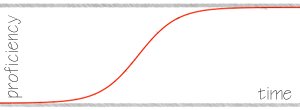
and can be modeled as the relation
proficiency = 1 / (1 + e-time)
Mathematically then, every member m in M has a proficiency mst in each skill s at time t, and that value will rise as they work with another member and acquire proficiency in that skill,
ms(t) = mst0 + psm / (1 + e-asm(t+t0))
where psm is a value designating the available incremental proficiency for a skill s that can be gained by a member m in a pair, asm is the rate of that gain, and t0 represents the point in time where acquisition begins. The greater the acquisition rate, the more quickly proficiency will be acquired.
The available incremental proficiency is related to the proficiency of member m and the combined proficiency of the pair when working with member mκ, and during acquisition is defined as
psmi = ((mist0 ⊕s mκst0) / mist0) - mist0
Higher values of psm indicate that there is more skill to be gained by the member than lower values. The ⊕s operator is used to represent that the incremental skill proficiency is not a pure sum of values, but is limited by proficiency overlap. If the highest level of proficiency for a given skill that can be achieved for a particular pair is some value ν, then gsm should be ν. If member mi of the pair has already achieved that level, mis will not grow further, but it should also not get smaller.
Going further it must be considered that the two team members working together may surpass the available incremental proficiency that would have been predicted at time t0. However, this is difficult to model without integrating statistics into the framework and will not be addressed here.
Every task w in W has an associated set of skills sw that are required to perform the task, and a contributing rate function wrs for each skill. The amount of skilled work wS that can be done in the time interval [t0, t] by an assigned pair of team members mi and mκ is given by
wS = Σsw ∫t0,t wrsmimκ ( mist0+mis(t) + mκst0+mκsa(t) )
= Σsw wrsmimκ ( (mist0+mκst0) + ∫t0,t (misa(t)+mκsa(t)) )
The wrs function is based on the proficiencies of the members in the assigned pair and the amount of proficient effort required by the task. The interesting part of the derivation is in the integral. As the work is being performed, skill acquisition is occurring, and proficiency and productivity are increasing.
Skill Atrophy
Just as a muscle will lose its strength when not exercised, so an unused skill will be slowly lost through time. Different skills are lost at different rates, and while it may take time to lose a skill completely, it will happen. What’s more each person will lose skills at different rates, so nothing is constant - except that without practice, over time skills will be lost by the team.
I call the atrophy of a skill backsliding. Like acquisition, backsliding starts slowly - the higher levels of proficiency can be recovered fairly quickly. But once it’s been a while since a skill has been used, it’s a slippery slope and proficiency degenerates quickly until it levels out. In the end, the memory of having once attained the skill is all that’s left. That isn’t saying the skill can’t be reacquired, and that acquisition may come more easily, but it is not immediately useful once the member has slid back down the forgetting curve.
The proficiency of a skill backslides when it starts to atrophy. For a team member and a skill, profieciency mst can be viewed mathematically as the opposite of skill acquisition when backsliding
ms(t) = mst0 - (bsm / (1 + e-dsm(t+t0)))
where bsm is a value designating the backsliding of proficiency for a skill s by a member m, and dsm is the incremental rate of loss for the skill and member. t0 represents the point in time where backsliding begins. It’s simple entropy. Left to the ravages of time, everything - including proficiency - degenerates.
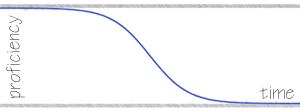
Note I am assuming here that mst0 ≤ bsm always holds. The consequence of mst0 > bsm is that with time a person can have negative skill. I can envision a couple of ways this might have meaning (like “If you want the job screwed up, give it to X!” for instance, or “working with Y will make you dumber!”) but these are outside the scope of this discussion.
And so with regard to proficiency being what it fortunately is, skills tend to backslide more slowly than they are acquired. For each person and skill, there’s an amount of time tsm that the proficiency of that skill will stick before it starts to backslide. And then once backsliding starts, the un-learning curve is not as steep.
What’s Manageable?
Everything taken together, it’s mathematically complex. Proficiency is a very individual thing for each person/skill combination. Given prioritized work, available team members to pair together, and the targeted set of skills that must be acquired and maintained, the question of when who should be doing what with whom is quite daunting.
While all of the terms that have been discussed are known, they are not manageable. They are qualities specific to team members, skills and work. Each member will have different values governing their learning and forgetting curves, and there will be many different skills that are being acquired while others are backsliding. Additionally, each piece of work requires proficiency in different skills.
Think of it as a problem in a three dimensional space, Members × Skills × Work, with multiple coefficients and values at every point in that volume that change over time. Assuming team members must have strong proficiency for a required set of skills, work needs to be assigned to pairs that will target attaining and maintaining the targeted proficiency level for each member and skill. Skill proficiency will begin to slowly backslide when the use of that skill ends, so refreshing skills periodically must be planned. Team members must keep doing the right work in the right pairs to keep the right skills from slipping away.
For each skill, a member’s proficiency mst as work gets done looks something like
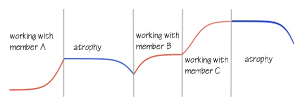
So the proficiency is a series of pieces corresponding to periods of improving skill while pairing, and atrophy when not. In this diagram, a member first pairs with another A on a project for two months, and skills rise. On the upward curve, they finish and the skill goes unused and begins to atrophy after a few months. But then the member pairs with B for six weeks, acquiring skill to their available incremental proficiency, and then with C for another six weeks, with whom the member can and does attain higher proficiency, as the member and C have a higher available incremental proficiency. Finally, the member starts something else and the skill goes unused and after a few months begins to atrophy again.
All that is effectively manageable is the assignment of team members to pairs and what tasks they will work on when. While it would certainly be possible to precisely plan and track skill proficiency for a team over time, and have team members who had the needed skills required to deliver the assigned work on time, a smart manager knows that all this math cannot be done by hand. It is too big an iterative optimization problem. And currently there is no software solution available to help.
So some simplification must be done for all this to be useful. Three qualities are being optimized for each time period:
-
maximize the amount of work completed by the team, WT = ΣW wT performed in the time interval T,
-
maximize the team’s proficiency, MS = ΣM mS for the relevant subset of skills S, and
-
minimize the team’s skill deviation ME from aggregate level (measuring the root mean squared error of Ms and the ms values is reasonable.)
When this high-level view is taken and used to guide choices, things will come out well enough - the team should be sharp and ready.
How to Really Do It
Yes, I know it’s a lot of math and functions and subscripts and all. A smart manager would just think about doing things according to these two basic rules:
-
Try to pair members on projects that will raise the less-skilled member’s proficiency where they’re lacking. A wanting individual should be given work that provides the opportunity to acquire proficiency in skills they haven’t mastered from the other member of the team that have more proficiency in the targeted skills. This will tend to raise Ms and lower ME.
-
Try to pair members with skills that aren’t so far apart. If the relative skill difference is large, the high proficiency of the skilled member will be slowed more than if the relative skill difference was smaller. The less skilled member’s ms values will still rise, but initially Wt will be much lower and ME will be higher. Over time, as the less skilled member gains proficiency, ME will have leveled out somewhat and Wt will suffer less. Starting by pairing two members that have closer proficiencies will keep a lot of work flowing when they are skilled and keep less skilled workers from slowing delivery down while learning.
These rules of thumb will suffice in most situations, but a smart manager will know there are going to be times when things don’t go as planned. Suboptimal pairings may be forced due to absences and vacations, or it may be more important to raise a member’s proficiency more quickly at the expense of work throughput. Different situations call for alternative management.
It should also be fairly clear that skill requirements in work are at best estimated, and the contributing rate function wrs may only be a simple model rather than as complex as it acts in reality. Mathematical precision aside, good estimates and following the rules of thumb above will keep things moving in the right direction.
In the next part of this series, exceptions to these rules and other complications will be considered.
Appendix
Terms and their meanings.
| Term | Meaning |
|---|---|
| asm | member m’s rate of acquisition of skill s when paired |
| bsm | member m’s decremental proficiency of unused skill s |
| dsm | member m’s rate of backsliding of unused skill s |
| M | set of team members |
| ME | difference between team’s optimal and actual proficiency |
| MS | team’s proficiency for a subset of relevant skills |
| mst | member m’s proficiency of skill s at time t |
| ν | maximum mst for a given pair |
| psm | member m’s available incremental proficiency of skill s when paired |
| S | set of relevant skills |
| T | a time interval |
| t | time |
| W | set of prioritized work tasks |
| wS | amount of work that requires skills in a subset of relevant skills |
| wrs | work rate function for a pair requiring skill s |
| WT | work completed by team in interval T |
The subscripts i and κ are used to indicate particular individual members.
Download the free eBook



